|
|
Tech/Exploratory:
Time In Three Parts
A practical definition of ratio temporality
NOTE: This is an old version of this article. It has
been updated.
It now includes new content, such as information
about how ratio-temporality is employed in biological neural networks. This
inherently leads to an understanding of how ratio-temporality can be employed
in artificial neural networks as well.
The
newer version containing the new material about how ratio-temporality is
employed in biological neural-networks, and in ANNs made with the Netlab
development environment, is included in
the Netlab book
as Appendix C.
This online version will serve as a place to accumulate related resources
and references.
Dominic John Repici
09-June-2009 (obsolete, newer version available)
(C) Copyright 2004-2009 Dominic John Repici
ALL RIGHTS RESERVED
(v1.0m)
This article is © Copyright, Creativyst, Inc. 2004-2013 ALL RIGHTS
RESERVED.
Links to this article are always welcome.
However, you may not copy, modify, or distribute this work or any part of it
without first obtaining express written permission from Creativyst, Inc.
Production and distribution of derivative products, such as displaying this
content along with directly related content in a common browser view are
expressly forbidden!
Those wishing to obtain permission to distribute copies of this article or
derivatives in any form should
contact me.
Permissions printed over any code, DTD, or schema files are supported as our
permission statement for those constructs.
Abstract
This paper documents specific relationships between time, frequency, sequence,
and temporality and uses that understanding of those relationships to propose
an alternative narrow definition for the terms "temporal" and "temporality."
Comments and feedback are welcome.
Document conventions
All illustrations are currently text based and assume that the document is
being viewed in a fixed width font. This document will be very confusing unless
it is VIEWED IN A FIXED WIDTH FONT. If viewed as HTML the fixed width will be
defined in markup. Word processor formats will also define a fixed width font.
Much like "consciousness," everybody seems to know what the word "temporal"
means yet if you look around for a precise definition you may not be satisfied
with what you find.
Here's what the Oxford Dictionary says:
"of or relating to time."
The Merriam Webster online dictionary says:
"a: of or relating to time as distinguished from space
b: of or relating to the sequence of time or to a
particular time"
These are fine if all you need is "[it has something to do with] time." This
paper represents my attempt to define a more precise sense of the word
"temporal." My goal is to restrict the definition by explaining how temporal
"relates to time" as well as its relationship to other components of a set
loosely described by the phrase "relating to time."
As defined here:
Here are the more precise (restricted) definitions for the terms temporality
and temporal proposed and supported in this paper.
Temporality (noun):
a: That component of time and/or space which is neither sequence or
frequency. - That component of events in time and/or space that remains
after sequence and frequency are removed. - The condition of being
temporal.
b: The relative distances or times between events or entities in time or
space.
Temporal (adj):
a: Of or relating to that component of time and/or space which is
neither sequence or frequency.
b: Of or relating to the relative distances between events or entities in time
or space.
This paper does not propose replacing the existing definition of temporal. It
only proposes a stricter sense of the term for when the specific sense
described here is needed.
For contexts where the word temporal is likely to be confused with its usual,
more general definition, the sense described here may be qualified as
"ratio-temporal." The reason for use of the word ratio as the qualifier for
this stricter sense of temporal should become clear in this explanation.
Fourier series transforms and similar tools that follow, speak of a time domain
and a frequency domain. Many mathematical tools now exist which can convert
between these two domains.
If you ask "How well does the tool perform the function for which it was
designed?" the answer would usually be that the tool works exactly as it
should.
If you change the question to: "How well does the reversible function of the
tool represent observations of real world phenomena?" you then find that
information from the time domain is lost when you convert it to the frequency
domain.
Example 1:
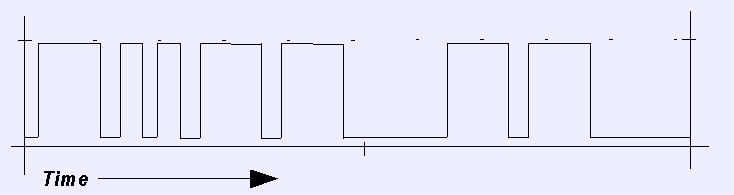 FIGURE 1:
A chart showing pulses representing a set of events in time. There is a
certain fractal nature to this (e.g., the 'up' and 'down' sides of each pulse
are also events), but for now, we will just assume events at the pulse level.
If you convert this from the time domain (shown) to the frequency domain,
information is lost. That is, this exact waveform will not be returned when
you convert it back to the time domain. Instead, the low- and high-frequency
components will probably be imposed over the entire reconstituted waveform.
This is the most important point to understand from this demonstration. If you
start with a representation in the frequency domain in the above example, you
can convert it to the time domain and back as many times as you'd like without
losing any of the original information. This reveals two things about the
relationship between the time domain and the frequency domain.
1. The time domain "encompasses" or "includes" the entire frequency domain
2. The frequency domain does NOT include the entire time domain.
In other words the relationship between the time and frequency domains is not
an equal one. If represented diagrammatically the frequency domain is
completely contained within the time domain (figure 3).
/---------------\
| Time |
| /---------\ |
| |Frequency| |
| \---------/ |
\---------------/
-Figure 3-
Expressed another way, we can say that frequency is a "component" of time. We
also know that there are other components because at least one thing gets lost
when we convert to frequency and back. In this case, we have seen that we lose
SEQUENCE, and as we will see we also lose at least one other constituent as
well (figure 4).
/-------------------------------------------\
| Time |
| /---------\ /-----------\ /---------\ |
| |Frequency| |Sequence | |Others? | |
| \---------/ \-----------/ \---------/ |
\-------------------------------------------/
-Figure 4-
As stated, this paper defines the temporal domain as a domain that exists
within the context of events in time, that is outside of the frequency, or
sequential components of the time domain. This relationship is shown
diagrammatically in Figure 5.
/-------------------------------------------\
| Time |
| /---------\ /-----------\ /---------\ |
| |Frequency| |Sequential | |Temporal | |
| \---------/ \-----------/ \---------/ |
\-------------------------------------------/
-Figure 5-
As you will see, the relationship between the temporal domain and the time
domain is similar to the relationship between the frequency domain and the time
domain. This will be documented now in order to show that the relationships
between time, frequency, sequential, and temporal domains diagrammed in figure
5 (above) are logically valid and usable for the purpose of supporting the
proposed definition of temporality.
This next illustration (Figure 6) will be used to relate the remainder of the
concepts in this paper. It is a graphic representation of events along a
time-line.
event name Q G A X L
time or space |--------------------------------------------->
-Figure 6-
This diagram depicts a series of five events occurring over a period of 41
equal intervals of time. It comprises frequency, sequence (order), and
temporality.
The amount of time each interval represents is not important; they could be
milliseconds, years, or millennia. Likewise the events could be the amplitude
levels of sine wave peaks or events in human history, the key is, it doesn't
matter what the actual events or interval lengths are. The labels we've given
are letters but should only be thought of as names for the events. They've
even been placed out of letter order to further emphasize that no alphabetic
order should be inferred. We could for example use pet names to label the
entities. We could have also represented the low and high waveform amplitudes
in example-1 as 'An' and 'Bn' respectively and spread them across the timeline
accordingly. Again, the point is, context is unimportant. Only events over
time are represented.
Sequence is that component of the time domain that embodies tense and
causality, though temporality may share in contributing to the phenominon of
causality.
There are components of frequency, sequence, and temporality in the time line
of Figure-6. As has been demonstrated above, converting to the frequency domain
and back will shed sequence.
Likewise, if you convert to the sequence domain and convert it back to the time
domain you will be left with.
QGAXL
This shows that you lose frequency information (you will be left with a single
frequency equal to the length of the sample interval). You also lose
temporality as it is defined in this paper.
Conversely, if we start from the sequence domain using the sequence QGAXL, we
can convert it to the time-domain and back with no loss of information from the
original (sequential) representation. This shows that just as in the case of the
FREQUENCY domain, the SEQUENCE domain is a sub-set, fully encompassed by the
time domain. This relationship is diagrammed in figures 4 and 5 (above).
Temporality is described here as the RATIOS of, or RELATIVE intervals between
events. The temporal domain carries no information about frequency or sequence.
Here's one way of representing the temporal domain from the time-line shown in
figure 6:
Q: G=2 A=3 X=7 L=8
G: Q=2 A=1 X=5 L=6
A: G=1 Q=3 X=4 L=5
X: Q=7 G=5 A=4 L=1
L: Q=8 G=6 A=5 X=1
-Figure 7-
There are a variety of notational conventions we can use. To construct this
notation I've counted the time intervals starting with the interval of the
first event (Q) up to the interval just before the second event (G) which
equaled 10 intervals. I continued on in similar fashion for each of the other
events. For simplicity's sake, I've divided all numbers gleaned by five for
the smallest whole number representation of the intervals. The resulting chart
is represented in Figure 7. This chart (Figure 7) can be simplified quite a
bit further but has been left completely filled in for clarity.
But isn't this holding sequential information? No, the sequence is only
revealed because of the way I've written it on the page. I don't have to write
it in that order though. Here's the same chart of temporal information but
presented without giving away any of the original sequence information.
A: Q=3 L=5 X=4 G=1
G: L=6 Q=2 A=1 X=5
L: G=6 Q=8 X=1 A=5
X: Q=7 A=4 G=5 L=1
Q: A=3 G=2 X=7 L=8
-Figure 8-
Ok, but frequency is preserved here isn't it? No. The only information carried
in the temporal domain are the distances between events RELATIVE to the
distances between other events (e.g. "There's twice as much time between A and
X as there is between G and Q"). The actual intervals could be microseconds,
years, or centuries among other things. The temporal representation retains no
hint of this (it could even be miles or light-years).
More to the point, the measured distance between any two events could be hours
in one observation and microseconds or years in the next observation. As long
as the RATIOS of measured distances between events remain the same, the
temporal domain representation will remain the same.
Figure 9A shows the temporal data converted back to the time domain. Note that
it covers a shorter period. We haven't preserved the original sample period so
the intervals themselves could represent a different amount of time as well.
The arrow key example in figure 9C (below) may be a little confusing. When
displayed on a terminal, put the cursor on the Q and use the arrow key to move
to the G. It doesn't matter if you go left then down or down then left, it
will be the same number of key-presses as you will use in the two diagrams
above it.
A:
event name Q GA XL
time or space |--------------------------------------------->
B:
It works backwards too:
event name LX---AG-Q
C:
or this way:
(arrow key -----Q
presses ----G-
on a ----A-
keyboard) LX----
-Figure 9-
This shows that, just as with the frequency and sequential domains, information
from the other two component domains is lost when we convert from the time
domain to the temporal domain and back. Also, if we start with only temporal
information we can convert back and forth between it and the time domain
without any loss of the original information.
As we have already shown, the other two component domains share a similar
relationship to the time domain. The relationships between the time domain and
its three component domains can be represented as shown in figure 5
(above).
Lastly, each of the frequency, sequential, and temporal domains do not seem to
overlap with the information about the time domain contained within their two
counterpart component domains.
Is it possible to use temporal relationships to predict the timing of future
events?
For example, we experiment and observe three "related" events. That is, we
make multiple observations, each with defferent absolute timings, but find
that they always exhibit the same temporal ratio.
X Y Z
t|--------------------------------------------->
Specifically, we note that they have this temporal component:
(X=Y:4 Z:6 | Y=X:4 Z:2 | Z=X:6 Y:2).
That is to say, period X<->Y is twice as long as period Y<->Z, and
period X<->Z is 3 times as long as the interval Y<->Z, etc.
Later we do more experiments and observe them again, perhaps with many
different absolute time intervals, but always with the same temporal
ratio:
X Y Z
t|--------------------------------------------->
And again and again with the same temporal ratio:
X YZ
t|--------------------------------------------->
X Y Z
t|--------------------------------------------->
The ratio relationships between the events should be
observed to remain roughly the same over many observations,
whether the absolute time-frame between X and Z spans a few
seconds, a few hours, or a few decades.
So, after many experiments we repeatedly see the same temporal
ratio relationships when observing these three events. We
establish a high probability that these are temporally
related events.
In this case, having established a temporal relationship we
can use observations of past event timing to predict when
a future event will occur.
NOW
| <--Past | Future-->
| X Y | Z
t|--------------------------------------------->
/
Prediction
(Y<->Z)=(X<->Y)/2
Again, whether the interval from the past (X<->Y) spans seconds,
hours, or years, the interval spanning into the future can be
predicted based on the previously observed ratio-temporal relationship
between the intervals.
Is causality exclusively an attribute of sequence ? While causality is
obviously embodied in sequence ("this follows that"), is it wrong to assume
that sequence is the ONLY component supporting the notion of causality? Is
there any possibility that cause-and-effect relationships exist between events
in the ratio-temporal domain as defined here?
That is, just as it can be assumed that one event can "cause" another event
that follows it sequentially, are there periods between events that can be
shown to "cause" time periods between other events?
That was rambling at best in pros, perhaps I can draw a picture:
To eliminate sequence from the prediction we made in the above section, we
should look for similar ratio-temporal relationships in events that can be
turned around.
For example, if after making the above observations, we now observe Z
following Y with a certain interval of time between them, can we assume,
based on our observations, that:
If they are "temporally related" then X will
occur in period Y<->Z * 2 after Y occurs? That
is, can we infer Y<->X = (Y<->Z)*2?
NOW
| <--Past | Future-->
| Z Y | X
t|--------------------------------------------->
\
Prediction
(Y<->X)=(Y<->Z)*2
Obviously this is a simplified and idealized picture. In the real world, we
may have some "slop" (error constant) in the measured interval differences.
Also, three events is the minimum number required for observing the strictly
defined ratio-temporality defined here. Three were used here purely for
simplicity and clarity.
One example of a more useful tactic might be to express the problem/solution
in terms of probability. For example, if we've measured a statistically valid
sample and observed the temporal ratios to be within +/-10% of their temporally
predicted periods, 100% of the time, then we can say our prediction has a
reasonable assurance of being accurate to within +/-10% of the predicted time
(where assurance is based primarily on the size of the previous sample).
If our sample shows that 98% of these events occur within 9% of their
temporally predicted times, then we can say that the odds of our predicted
time being accurate to within 9% is still reasonably assured, but less assured
than our prediction that it will occur within 10% of our prediction.
The assurance level, in each case, is based on the sample size, or the number
of past observations that came within the stated accuracy range.
. . .
Note 1: Are these three components irreducible? It seems as though the
three constituent components documented here: frequency, sequence, and
temporality are elemental components of (events in) time. It doesn't seem that
these three components can themselves be reduced any further, though, to be
honest, this is little more than a hunch, as I have not tried very hard to
further reduce these components.
. . .
Note 2: Are there any other components? Intuitively, it seems as
though you can also conclude that frequency, sequence, and temporality are the
complete set comprising the time domain. In other words, if you convert time
to these three domains, you will have enough information to precisely
reconstruct the original time domain (within limits defined only by your sample
rate).
. . .
Note 3: Is there any synergy in these components? There may be a way to
reconstruct one missing domain given the information from the other two. Can
it be done? And is there symmetry (works no matter which two you start with)?
. . .
Note 4: Representing context Question (speculation): will extra
dimensions, such as the addition of a second dimension in the arrow-key example
in figure-9C, introduce a possible consistent mechanism for representing
context?
I've had a fascination with neural networks and trying to keep up with our ever
growing understanding of how biological neural nets function since the 1980's.
While experimenting with neural network simulations there has often been a need
for a precisely defined understanding of the meaning of temporal and temporality
(or whatever it is that has been described here).
Clearly this paper takes some liberties. There is some presumption here as to
what the word temporal means. The excuse is also the same as the reason for
this paper being written. In twenty years of looking I've been unable to find
this sub-definition for the word "temporal" or what temporality is. If there
is a better fitting word for the concept described here, please let me know.
I'd be more than happy to use it.
Also, though temporality is not in itself a part of neural network technology,
the lack of a labeled understanding for the concept described here (or my
inabillity to find one) has been a constant obstacle over the years in various
attempts to better understand neural networks.
So, with that bit of cautious, tentative, confidence that this wheel just isn't
out there, I've decided to invent my own here. Apologies to anyone who, like me,
cringes at this. You may find some solace in knowing that this article is not
proposing a replacement definition, just a more restricted sense of the word for
when context requires.
This is important to note. The roadblocks that have emerged needed a definition of
the concept of ratio-temporality in GENERAL terms, so this paper seeks to define
ratio-temporality in GENERAL terms. How that definition relates to neural networks
is outside of the scope of this paper.
If you know of anyone out there who has tackled this subject matter already
(likely better than I), you will find a grateful student if you could deliver
a note stating where to find the material. If you can help, or if you'd just
like to discuss it, contact me.
time 1 2 3 4 5
interval 1234567890123456789012345678901234567890123456789012345
event name Q G A X L
-Figure 10-
Haiku: New Seasons
. . .
Not the intervals
But how they are related
Temporality
Netlab (A0) version 0.1
April 1990 D. John Repici
Netlab v 0.1 is my very early (and first) attempt at a neural network
simulation program along with some documentation. The documentation and small
test networks include some rudimentary experiments and speculation about how
temporal phenomena may play a part in biological neural network learning and
operation. This was distributed in April of 1990 on the AI-Expert forum on
Compuserve and shortly after on the AI forum on GEnie. Distributions from the
AI-Expert forum can still be found on the Fido network.
FIGURE 1:
A chart showing pulses representing a set of events in time. There is a
certain fractal nature to this (e.g., the 'up' and 'down' sides of each pulse
are also events), but for now, we will just assume events at the pulse level.
If you convert this from the time domain (shown) to the frequency domain,
information is lost. That is, this exact waveform will not be returned when
you convert it back to the time domain. Instead, the low- and high-frequency
components will probably be imposed over the entire reconstituted waveform.
This is the most important point to understand from this demonstration. If you
start with a representation in the frequency domain in the above example, you
can convert it to the time domain and back as many times as you'd like without
losing any of the original information. This reveals two things about the
relationship between the time domain and the frequency domain.
1. The time domain "encompasses" or "includes" the entire frequency domain
2. The frequency domain does NOT include the entire time domain.
In other words the relationship between the time and frequency domains is not
an equal one. If represented diagrammatically the frequency domain is
completely contained within the time domain (figure 3).
/---------------\
| Time |
| /---------\ |
| |Frequency| |
| \---------/ |
\---------------/
-Figure 3-
Expressed another way, we can say that frequency is a "component" of time. We
also know that there are other components because at least one thing gets lost
when we convert to frequency and back. In this case, we have seen that we lose
SEQUENCE, and as we will see we also lose at least one other constituent as
well (figure 4).
/-------------------------------------------\
| Time |
| /---------\ /-----------\ /---------\ |
| |Frequency| |Sequence | |Others? | |
| \---------/ \-----------/ \---------/ |
\-------------------------------------------/
-Figure 4-
As stated, this paper defines the temporal domain as a domain that exists
within the context of events in time, that is outside of the frequency, or
sequential components of the time domain. This relationship is shown
diagrammatically in Figure 5.
/-------------------------------------------\
| Time |
| /---------\ /-----------\ /---------\ |
| |Frequency| |Sequential | |Temporal | |
| \---------/ \-----------/ \---------/ |
\-------------------------------------------/
-Figure 5-
As you will see, the relationship between the temporal domain and the time
domain is similar to the relationship between the frequency domain and the time
domain. This will be documented now in order to show that the relationships
between time, frequency, sequential, and temporal domains diagrammed in figure
5 (above) are logically valid and usable for the purpose of supporting the
proposed definition of temporality.
This next illustration (Figure 6) will be used to relate the remainder of the
concepts in this paper. It is a graphic representation of events along a
time-line.
event name Q G A X L
time or space |--------------------------------------------->
-Figure 6-
This diagram depicts a series of five events occurring over a period of 41
equal intervals of time. It comprises frequency, sequence (order), and
temporality.
The amount of time each interval represents is not important; they could be
milliseconds, years, or millennia. Likewise the events could be the amplitude
levels of sine wave peaks or events in human history, the key is, it doesn't
matter what the actual events or interval lengths are. The labels we've given
are letters but should only be thought of as names for the events. They've
even been placed out of letter order to further emphasize that no alphabetic
order should be inferred. We could for example use pet names to label the
entities. We could have also represented the low and high waveform amplitudes
in example-1 as 'An' and 'Bn' respectively and spread them across the timeline
accordingly. Again, the point is, context is unimportant. Only events over
time are represented.
Sequence is that component of the time domain that embodies tense and
causality, though temporality may share in contributing to the phenominon of
causality.
There are components of frequency, sequence, and temporality in the time line
of Figure-6. As has been demonstrated above, converting to the frequency domain
and back will shed sequence.
Likewise, if you convert to the sequence domain and convert it back to the time
domain you will be left with.
QGAXL
This shows that you lose frequency information (you will be left with a single
frequency equal to the length of the sample interval). You also lose
temporality as it is defined in this paper.
Conversely, if we start from the sequence domain using the sequence QGAXL, we
can convert it to the time-domain and back with no loss of information from the
original (sequential) representation. This shows that just as in the case of the
FREQUENCY domain, the SEQUENCE domain is a sub-set, fully encompassed by the
time domain. This relationship is diagrammed in figures 4 and 5 (above).
Temporality is described here as the RATIOS of, or RELATIVE intervals between
events. The temporal domain carries no information about frequency or sequence.
Here's one way of representing the temporal domain from the time-line shown in
figure 6:
Q: G=2 A=3 X=7 L=8
G: Q=2 A=1 X=5 L=6
A: G=1 Q=3 X=4 L=5
X: Q=7 G=5 A=4 L=1
L: Q=8 G=6 A=5 X=1
-Figure 7-
There are a variety of notational conventions we can use. To construct this
notation I've counted the time intervals starting with the interval of the
first event (Q) up to the interval just before the second event (G) which
equaled 10 intervals. I continued on in similar fashion for each of the other
events. For simplicity's sake, I've divided all numbers gleaned by five for
the smallest whole number representation of the intervals. The resulting chart
is represented in Figure 7. This chart (Figure 7) can be simplified quite a
bit further but has been left completely filled in for clarity.
But isn't this holding sequential information? No, the sequence is only
revealed because of the way I've written it on the page. I don't have to write
it in that order though. Here's the same chart of temporal information but
presented without giving away any of the original sequence information.
A: Q=3 L=5 X=4 G=1
G: L=6 Q=2 A=1 X=5
L: G=6 Q=8 X=1 A=5
X: Q=7 A=4 G=5 L=1
Q: A=3 G=2 X=7 L=8
-Figure 8-
Ok, but frequency is preserved here isn't it? No. The only information carried
in the temporal domain are the distances between events RELATIVE to the
distances between other events (e.g. "There's twice as much time between A and
X as there is between G and Q"). The actual intervals could be microseconds,
years, or centuries among other things. The temporal representation retains no
hint of this (it could even be miles or light-years).
More to the point, the measured distance between any two events could be hours
in one observation and microseconds or years in the next observation. As long
as the RATIOS of measured distances between events remain the same, the
temporal domain representation will remain the same.
Figure 9A shows the temporal data converted back to the time domain. Note that
it covers a shorter period. We haven't preserved the original sample period so
the intervals themselves could represent a different amount of time as well.
The arrow key example in figure 9C (below) may be a little confusing. When
displayed on a terminal, put the cursor on the Q and use the arrow key to move
to the G. It doesn't matter if you go left then down or down then left, it
will be the same number of key-presses as you will use in the two diagrams
above it.
A:
event name Q GA XL
time or space |--------------------------------------------->
B:
It works backwards too:
event name LX---AG-Q
C:
or this way:
(arrow key -----Q
presses ----G-
on a ----A-
keyboard) LX----
-Figure 9-
This shows that, just as with the frequency and sequential domains, information
from the other two component domains is lost when we convert from the time
domain to the temporal domain and back. Also, if we start with only temporal
information we can convert back and forth between it and the time domain
without any loss of the original information.
As we have already shown, the other two component domains share a similar
relationship to the time domain. The relationships between the time domain and
its three component domains can be represented as shown in figure 5
(above).
Lastly, each of the frequency, sequential, and temporal domains do not seem to
overlap with the information about the time domain contained within their two
counterpart component domains.
Is it possible to use temporal relationships to predict the timing of future
events?
For example, we experiment and observe three "related" events. That is, we
make multiple observations, each with defferent absolute timings, but find
that they always exhibit the same temporal ratio.
X Y Z
t|--------------------------------------------->
Specifically, we note that they have this temporal component:
(X=Y:4 Z:6 | Y=X:4 Z:2 | Z=X:6 Y:2).
That is to say, period X<->Y is twice as long as period Y<->Z, and
period X<->Z is 3 times as long as the interval Y<->Z, etc.
Later we do more experiments and observe them again, perhaps with many
different absolute time intervals, but always with the same temporal
ratio:
X Y Z
t|--------------------------------------------->
And again and again with the same temporal ratio:
X YZ
t|--------------------------------------------->
X Y Z
t|--------------------------------------------->
The ratio relationships between the events should be
observed to remain roughly the same over many observations,
whether the absolute time-frame between X and Z spans a few
seconds, a few hours, or a few decades.
So, after many experiments we repeatedly see the same temporal
ratio relationships when observing these three events. We
establish a high probability that these are temporally
related events.
In this case, having established a temporal relationship we
can use observations of past event timing to predict when
a future event will occur.
NOW
| <--Past | Future-->
| X Y | Z
t|--------------------------------------------->
/
Prediction
(Y<->Z)=(X<->Y)/2
Again, whether the interval from the past (X<->Y) spans seconds,
hours, or years, the interval spanning into the future can be
predicted based on the previously observed ratio-temporal relationship
between the intervals.
Is causality exclusively an attribute of sequence ? While causality is
obviously embodied in sequence ("this follows that"), is it wrong to assume
that sequence is the ONLY component supporting the notion of causality? Is
there any possibility that cause-and-effect relationships exist between events
in the ratio-temporal domain as defined here?
That is, just as it can be assumed that one event can "cause" another event
that follows it sequentially, are there periods between events that can be
shown to "cause" time periods between other events?
That was rambling at best in pros, perhaps I can draw a picture:
To eliminate sequence from the prediction we made in the above section, we
should look for similar ratio-temporal relationships in events that can be
turned around.
For example, if after making the above observations, we now observe Z
following Y with a certain interval of time between them, can we assume,
based on our observations, that:
If they are "temporally related" then X will
occur in period Y<->Z * 2 after Y occurs? That
is, can we infer Y<->X = (Y<->Z)*2?
NOW
| <--Past | Future-->
| Z Y | X
t|--------------------------------------------->
\
Prediction
(Y<->X)=(Y<->Z)*2
Obviously this is a simplified and idealized picture. In the real world, we
may have some "slop" (error constant) in the measured interval differences.
Also, three events is the minimum number required for observing the strictly
defined ratio-temporality defined here. Three were used here purely for
simplicity and clarity.
One example of a more useful tactic might be to express the problem/solution
in terms of probability. For example, if we've measured a statistically valid
sample and observed the temporal ratios to be within +/-10% of their temporally
predicted periods, 100% of the time, then we can say our prediction has a
reasonable assurance of being accurate to within +/-10% of the predicted time
(where assurance is based primarily on the size of the previous sample).
If our sample shows that 98% of these events occur within 9% of their
temporally predicted times, then we can say that the odds of our predicted
time being accurate to within 9% is still reasonably assured, but less assured
than our prediction that it will occur within 10% of our prediction.
The assurance level, in each case, is based on the sample size, or the number
of past observations that came within the stated accuracy range.
. . .
Note 1: Are these three components irreducible? It seems as though the
three constituent components documented here: frequency, sequence, and
temporality are elemental components of (events in) time. It doesn't seem that
these three components can themselves be reduced any further, though, to be
honest, this is little more than a hunch, as I have not tried very hard to
further reduce these components.
. . .
Note 2: Are there any other components? Intuitively, it seems as
though you can also conclude that frequency, sequence, and temporality are the
complete set comprising the time domain. In other words, if you convert time
to these three domains, you will have enough information to precisely
reconstruct the original time domain (within limits defined only by your sample
rate).
. . .
Note 3: Is there any synergy in these components? There may be a way to
reconstruct one missing domain given the information from the other two. Can
it be done? And is there symmetry (works no matter which two you start with)?
. . .
Note 4: Representing context Question (speculation): will extra
dimensions, such as the addition of a second dimension in the arrow-key example
in figure-9C, introduce a possible consistent mechanism for representing
context?
I've had a fascination with neural networks and trying to keep up with our ever
growing understanding of how biological neural nets function since the 1980's.
While experimenting with neural network simulations there has often been a need
for a precisely defined understanding of the meaning of temporal and temporality
(or whatever it is that has been described here).
Clearly this paper takes some liberties. There is some presumption here as to
what the word temporal means. The excuse is also the same as the reason for
this paper being written. In twenty years of looking I've been unable to find
this sub-definition for the word "temporal" or what temporality is. If there
is a better fitting word for the concept described here, please let me know.
I'd be more than happy to use it.
Also, though temporality is not in itself a part of neural network technology,
the lack of a labeled understanding for the concept described here (or my
inabillity to find one) has been a constant obstacle over the years in various
attempts to better understand neural networks.
So, with that bit of cautious, tentative, confidence that this wheel just isn't
out there, I've decided to invent my own here. Apologies to anyone who, like me,
cringes at this. You may find some solace in knowing that this article is not
proposing a replacement definition, just a more restricted sense of the word for
when context requires.
This is important to note. The roadblocks that have emerged needed a definition of
the concept of ratio-temporality in GENERAL terms, so this paper seeks to define
ratio-temporality in GENERAL terms. How that definition relates to neural networks
is outside of the scope of this paper.
If you know of anyone out there who has tackled this subject matter already
(likely better than I), you will find a grateful student if you could deliver
a note stating where to find the material. If you can help, or if you'd just
like to discuss it, contact me.
time 1 2 3 4 5
interval 1234567890123456789012345678901234567890123456789012345
event name Q G A X L
-Figure 10-
Haiku: New Seasons
. . .
Not the intervals
But how they are related
Temporality
Netlab (A0) version 0.1
April 1990 D. John Repici
Netlab v 0.1 is my very early (and first) attempt at a neural network
simulation program along with some documentation. The documentation and small
test networks include some rudimentary experiments and speculation about how
temporal phenomena may play a part in biological neural network learning and
operation. This was distributed in April of 1990 on the AI-Expert forum on
Compuserve and shortly after on the AI forum on GEnie. Distributions from the
AI-Expert forum can still be found on the Fido network.
- Related Papers and Links:
Related Blog and Glossary Entries at Stand Out Publishing:
This article is © Copyright, Creativyst, Inc. 2004 - 2013 ALL RIGHTS
RESERVED.
Links to this article are always welcome.
However, you may not copy, modify, or distribute this work or any part of it
without first obtaining express written permission from Creativyst, Inc.
Production and distribution of derivative products, such as displaying this
content along with directly related content in a common browser view are
expressly forbidden!
Those wishing to obtain permission to distribute copies of this article or
derivatives in any form should
contact me.
Permissions printed over any code, DTD, or schema files are supported as our
permission statement for those constructs.
|
|